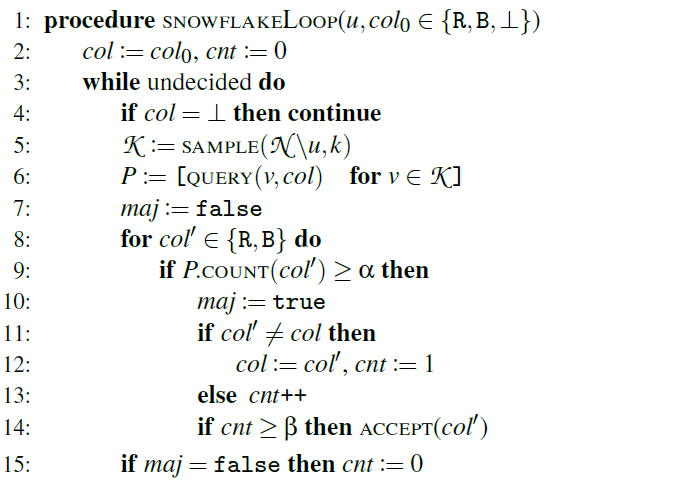Avalanche 共识协议详解

本文对雪崩共识协议簇进行介绍。该协议簇是一系列无主拜占庭容错协议，使用基于网络重复随机采样的亚稳态机制构建。雪崩协议能够在存在拜占庭节点的情况下提供强概率安全保证，且并发和无主性质使其能够实现高吞吐量和高可扩展。

协议主要目标：

• 绿色 (green)：能源消耗很少。

• 静止 (quiescent)：没有交易时不需要工作（出块）。

• 高效 (efficient)：节点交互复杂度 O(knlogn) ~ O(kn)。

如何实现以上目标？主要依赖以下几种措施：

• 并行共识模型：不使用单一复制状态机 (RSM) 模型，每个节点维护自己的RSM（可以互相转移所有权），系统对有关联的交易只维护偏序。

• 重复随机采样：引导诚实节点产生相同输出。

• 亚稳态决策：亚稳态决策可以使得一个大网络快速推进到一个不可逆的状态。

该算法可以提供强概率安全性保证，并且保证诚实节点的活性。所谓“强概率安全保证”，是指共识被逆转的可能性小到可以被忽略（甚至小于哈希碰撞的概率），实际上 PoW 提供的也是强概率安全性保证。

1 基础

首先介绍下文中的一些基本概念。

在任何基于复制状态机 (Replicated State Machine, RSM) 的分布式系统，都需要满足两个特性，即安全性和活性，文中定义如下：

P1. Safety. No two correct nodes will accept conflicting transactions.

P2. Liveness. Any transaction issued by a correct client (aka virtuous transaction) will eventually be accepted by every correct node.

2 Slush（雪泥）

论文首先提出了名为 Slush 的共识算法，也是整个协议簇中最简单最基础的部分。Slush 是非拜占庭协议，意味着其不能容忍作恶节点的存在。作者抽象出一个染色问题：任何时刻所有节点可能处于 $\lbrace red,blue,⊥\rbrace$ 三种状态之一，共识就是如何通过节点间的通信使得所有节点最终的颜色一致。

Slush 算法描述如下：

详细分析：

1. 在起始时刻，所有节点都是未着色状态；
2. 节点 $u$ 循环发起查询，总共 $m$ 轮，每轮随机选择 $k$ 个样本发送包含自身颜色的查询；
3. 当其他节点 $v$ 收到一个查询时，则返回一个包括自己颜色的响应，如果此时节点 $v$ 还是未着色状态，则先将查询中的颜色更新为自己的颜色再响应；
4. 一旦收集到 $k$ 个响应，节点 $u$ 判断是否存在某个颜色数大于等于 $αk$，$α > 0.5$ 表示一个协议参数。如果存在某个颜色满足该阈值则将自身颜色更新为该颜色；
5. 如果没有在限定时间收集到 $k$ 个响应，则 $u$ 重新采样发送查询，直至收集到 $k$ 个响应

Slush 有如下优点：

• 无记忆，每轮之间节点除了自身颜色不记录额外信息；
• 小样本采样，不同于其他算法需要对所有节点发送请求，Slush 只需要发送 $k$ 个请求；
• 抗亚稳态，即便是 50/50 的初始状态，也可以通过采样的随机扰动打破平衡，然后反复采样放大优势；
• 如果 $m$ 足够大，算法可以保证所有节点都有同等机会被染色；

但是 Slush 并不能提供足够强的拜占庭安全保证，如果存在拜占庭节点故意将自身颜色变成和主流颜色不一样，则可能打乱平衡。因此 Slush 并不是 BFT，但为后续机制提供了基础。

3 Snowflake（雪花）

相比 Slush，第二个算法 Snowflake 做了进一步改进：

详细分析：

1. 每个节点引入了一个计数器 $cnt$ 变量，初始 $cnt=0$，每当一轮查询返回的 $k$ 个响应某个颜色 $col ≥ αk$，则将其 $cnt+1$ ；
2. 如果满足条件的颜色和自身颜色不同，则将自身颜色设定为该颜色，并且重置 $cnt$；
3. 引入另一个安全系数 $β$ ，当 $cnt$ 大于 $β$ 时，则最终确定该节点颜色，而不需要执行 $m$ 次查询。

当给定一个 $ε$-guarantee 的拜占庭环境，Snowflake 可以保证安全性和活性。

4 Snowball（雪球）

Snowflake 记忆的状态是短暂的，每次颜色变化都会将计数器清零。为了使得系统更加难以被攻击，Snowball 增加了一个置信度计数器 (confidence counter) 。算法具体如下：

详细分析：

1. 对每个颜色都增加一个置信度计数器，例如 $d[R]$、$d[B]$；
2. 每当一轮查询返回的 $k$ 个响应某个颜色 $col’ ≥ αk$，将该颜色的 $d[col’] + 1$，如果 $d[col’]$ 最大，则将自身 $col$ 更变为该 $col’$；
3. 进一步地，如果 $col’$ 和上次响应 通过阈值的 lastcol 不一样，则更新 lastcol 为 $col’$，并且重置 $cnt$；
4. 如果 $col’$ 和上次响应通过阈值的 $lastcol$ 一样，则 $cnt+1$ ，当 $cnt$ 大于 $β$ 时，则最终确定该节点颜色。

总的来说，Snowball 中仍然是连续 $β$ 满足阈值条件的颜色才可能成为最终颜色，但置信度计数器的引入保证了最终确定的颜色同样具有高信任度。

5 Avalanche DAG（雪崩）

作为论文中协议簇的最终版本，Avalanche 将 Snowball 拓展为 multi-decree protocol。

Avalanche 在 Snowball 的基础上引入了有向无环图 (DAG) 的存储结构，即在冲突集中使用 Snowball 协议共识出一笔交易。这会带来两点好处：

• 更高效：对 DAG 某个顶点的投票隐含了对“从创世顶点到该顶点”这整条链的认可。

• 更安全：DAG 把各个交易的命运交织在了一起，因此共识更加难以被逆转（需要更多诚实节点的认可）。

首先解释一下几个术语：

• 祖先集 (ancestor set)：每个交易可能有一到多个父交易，从它们的父交易一直追溯到创世顶点过程中的所有交易组成该交易的祖先集。

• 子孙集 (progeny set)：该交易的所有子孙后代交易的集合。

• 冲突集 (conflict set)：如果两笔或多笔交易发生了冲突（例如使用了同样的 UXTO 输入，即双花），那么它们组成一个冲突集。

• 凭证 (chit)：如果某笔交易查询成功（超过阈值），则称该交易收到了一个凭证，否则凭证值为 0 。

为了适用于资产交易这样的真实场景，Avalanche 相比前三个算法引入了很多新概念，具体如下：

• $\mathcal{T}_u$ 表示节点 $u$ 内所记录的所有交易集合；

• $\mathcal{P}_T$ 表示所有和交易 $T$ 冲突的交易集合（$P_T$ 应该包括 $T$ 本身）

  比如两个冲突的交易 $T_i$ 和 $T_j$ ，由于冲突具有传递性，有 $\mathcal{P_{T_i}}=\mathcal{P_{T_j}}$ ，每个冲突交易集都有 $pref$ 和 $cnt$ 两个属性，简单地说这些都跟交易 $T$ 的置信度相关，具体后文会详细介绍。

• $T’\leftarrow T$ 表示交易 $T$ 的父交易是 $T’$ ；

• $T’\leftarrow^* T$ 表示从在至少一条路径从交易 $T$ 到交易 $T’$ 。

图中，每个方块表示一笔交易，具有一对 <chit, confidence> ，可以看到颜色更深的方块置信度更高。而每个交易都有一个冲突交易集，例如 $T_9$、$T_6$ 和 $T_7$ 属于同一个冲突交易集，即 $P_{T_9} = P_{T_6} = P_{T_7}$，但由于 $T_9$ 具有更高的置信度，因此该交易集的优先交易 (preferred tx) 为 $T_9$。

Avalanche 会将每笔交易存储在一个 DAG 中，DAG 中每个元素可能有多个父交易，并且需要注意的是父子关系不代表在应用层面相互依赖。

为了避免共识结果中包含冲突交易，在 Avalanche 中定义了冲突集，Avalanche 中的每笔交易都属于一个冲突集，冲突集中也只能有一笔交易，每个冲突集就是一个 Snowball 实例，但是置信度的计算方式略有不同，某笔交易的置信度是所有子孙交易的凭证值之和（$c$ 表示凭证，$d$ 表示置信度）。

每个节点需使用 Snowball 协议从冲突集中共识出一笔交易，当这笔交易的置信度达到一个阈值时，即可认为这笔交易被最终确定了。

具体流程：

初始化

上面提到每个 $P_T$ 包括了 $pref$ 和 $cnt$ 两个属性，初始化的 $P_T$ 只有 $T$ 本身，因此 $P_T.pref = T，P_T.cnt = 0$。当后续收到更多冲突交易后， $P_T$ 集合增加，$pref$ 和 $cnt$ 的更新则发生在收到响应 后。

查询和响应

详细分析：

1. 节点 $u$ 找到新交易 $T$（还未确定的交易，即 $T ∈ \mathcal{T} ∧ T ∉ \mathcal{Q}$），启动一轮查询，即随机采样 $k$ 个节点发送包括该 $T$ 的查询，注意此处查询中实际上包含了 $T$ 和以及在 DAG 中所有 $T$ 可达的其他交易；
2. 对收到查询的节点而言，如果查询中的 $T$ 以及其祖先交易在其冲突集中是优先选项 (preferred option)，则返回 yes-vote，反之则返回 no-vote；
3. 节点 $u$ 收集返回的 $k$ 个响应，如果该 $T$ 满足阈值（即有超过 $αk$ 个节点返回认可该交易的响应），则该交易的 $cT$ 赋值为 1（获得一个凭证），并且更新 $T$ 交易所有祖先交易 $T’$ 对应 $P_{T’}$ 的 $pref$ 和 $cnt$；
4. 类似 Snowball，节点 $u$ 对 $T$ 有一个置信度值，其计算方法如下：

\[d_u(T)=\sum_{T'\in\mathcal{T}_u, T\leftarrow^*T'} c_{uT'}\]

简单地说就是交易 $T$ 的 $d(T)$ 等于其所有后代交易的 $cT’$ 之和，凭证的获取方式见第三步。需要指出的是，任何交易的凭证只可能为 0 或 1，但随着 DAG 规模的不断增长，$dT$ 也会随着其后代的增加而表现出单调增特性。

这里再详细介绍下第二步中，查询返回的机制。当其他节点收到 $u$ 发送的查询后，在 DAG 中找到 $T$ 的所有祖先交易 $T’$ ，如果每个 $T’$ 在其冲突交易集合 $P_{T’}$ 中都处于优先状态，则返回一个 yes-vote，反之返回 no-vote。具体描述如下：

那么，什么时候应用可以接受 (accept) 或者提交 (commit) 一笔交易呢？Avalanche 把对最终交易的接受点和决定权交给了应用层。应用层通过自己定义的谓词 (predicate)，把接受交易的风险加入考虑。

• 如果冲突集中只有一笔交易（即没有冲突），置信度超过 $β_1$ 即可提交，称为“安全早期提交 (safe early commit) ”

• 否则，如果冲突集中有多笔交易，根据 Snowball 协议，需要收到超过 $β_2$ 个连续查询回复才可以提交

至此，Avalanche 整个流程介绍完毕。

6 分析

通信复杂度

• Snowflake & Snowball: O(knlogn)

• Avalanche: 每个节点O(k), 总复杂度O(kn)

两大创新

Avalanche 中的两大创新分别是：

• 子采样 (subsampling)：通信成本低。无论是 20 个节点还是 2000 个节点，某个节点发送的共识信息数量是恒定的。

• 传递性投票 (transitive voting)：即给某个顶点投票等同于给该顶点的所有祖先顶点投票，这样有助于提升交易吞吐量。每个节点实际上集合了很多投票。

可能存在的问题

1. 随机采样达到的是非确定性共识

   随机数对于区块链技术来说很关键。本质上，分布式账本的核心问题就是随机选择出块人的问题，这个随机性要能被全网确认，并且不能被操控，也不能被预测，否则恶意节点可以通过操控这个随机数从而达到操控整个链。在 Avalanche 中，随机采样是非常关键的，但是对怎么随机采样却没有像 Algorand 那样详细地描述，随机抽到样本的整体代表性也没有详细的理论论证，因此其所达成的共识只是一种概率性的共识，并非确定性共识。

2. 冲突交易不受保护

   如果用户不小心将一笔交易发送了两次，Avalanche 是无法在这两种交易之间做出选择的，会直接导致这笔钱丢失，这点被 Avalanche 当成能抵御双花攻击来做宣传，但是实际应用中，用户无任何主观恶意下，不小心将一笔交易点击两次发送的情况还是会经常发生，如果直接将用户资金丢失的话，每次发送交易都得非常小心并等待系统回复才行，这将大大降低交易的速度。

3. 需要大量参与者的支持

   随机采样所达到的共识必须依赖大量的节点支持才能算是有效，并且这些节点还得时刻保持在线，以便被随机抽取到，这在现实的自由网络下是不太现实的，如果采用云服务器的方式，整个网络运作成本将会非常高。